18新利最新登入博弈论如何运作

在前一节中，我们研究了囚徒然后把它画在矩阵上。这是a的一个例子simultaneous-move游戏。游戏要么是同步移动，要么sequential-move游戏。在同时移动游戏中，双方在不知道对方移动的情况下进行移动。盲目拍卖就是这样运作的，合同竞标也是如此。在顺序移动游戏中，玩家轮流移动，就像国际象棋或谈判一样。

对于两个玩家同时移动的游戏，我们必须假设我们的对手会寻求最好的结果。因此，我们也必须尽可能采取最有利的行动来保护自己。如果囚徒困境是按顺序而不是同时进行，玩家会选择不同的策略吗?

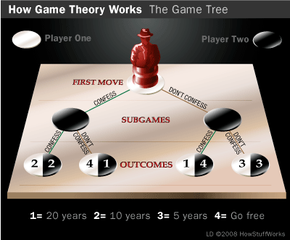
虽然同时移动游戏可以绘制在矩阵上，但顺序移动游戏可以绘制在矩阵上博弈树。在博弈树上绘制的囚徒困境是这样的:

移动的顺序在树中从上到下表示。的最节点表示参与人1的第一步(坦白或不坦白)。它下面的两个节点是现在进行。每个代表参与人2对第一步的可能反应。下面一行的四个节点是终端节点表示这个博弈的所有四种可能的结果。

我们可以用这种形式来研究博弈并为参与人2选择最佳策略。这让我们能够反向确定参与人1应该采取什么行动，并知道参与人2在两种情况下的理性行为。18新利最新登入这种从端到端观察游戏的过程叫做逆向归纳。我们看到参与人2的最佳策略是坦白，不管参与人1的开局如何。通过将我们的分析进一步向上移动到游戏的开始，我们知道参与人1必须选择背叛(忏悔)。

我们看到，在像囚徒困境这样的单次博弈中，同时进行或顺序进行并不会改变每个参与者的最佳策略。

在下一节中，我们将学习为什么当我们一次又一次地玩囚徒困境时，完全理性的自私必须被扔到窗外。