即使最聪明的数学家不能解决Collatz猜想

Collatz猜想,“3 n + 1问题,”我们仍在等待解决。介绍了1937年由德国数学家洛萨Collatz,Collatz猜想是一个看似简单的问题与惊人的难以捉摸的回答。猜想假设如果你重复两个简单的算术运算,最终你会将每个正整数转换成一个数量。问题是,它还没有被证明是适用于所有整数。也许有一些数字序列急驰到无穷。

数学家已经测试了数以百万计的自然数,没有人证明它错了。但是没有人无条件地证明它正确。传奇匈牙利数学家保罗鄂尔多斯引用说,“数学可能没有准备好这样的问题。”

Collatz想出了他的猜想两年在收到柏林大学的博士学位。对那些做了很多重要的数学在他的职业生涯中,他以一个新奇的问题——一个可以测试由一群四年级——是非凡的。虽然所有计算支持的猜想是正确的,事实上它仍然没有解决86年使其更加有趣。

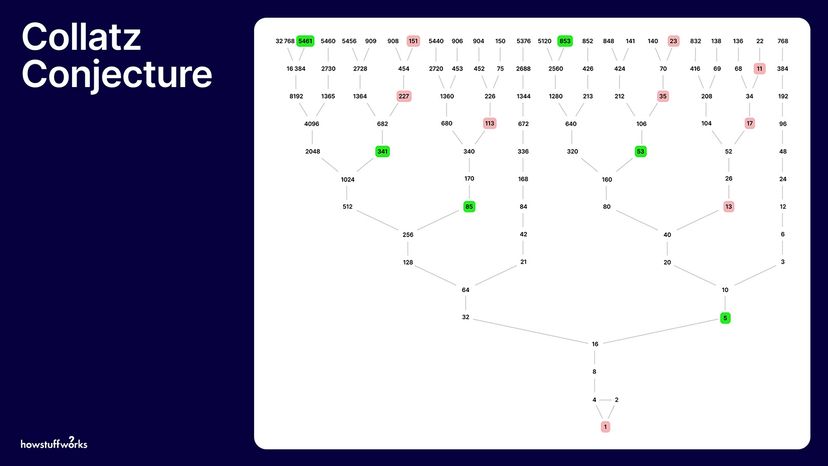
Collatz序列也被称为“3 n + 1“序列,因为它是由从任何正数,只是两个简单的规则:如果是偶数,除以2,如果是奇数,并添加一个三倍。因此,“3 n + 1”。Follow those two rules over and over, and the conjecture states that, regardless of the starting number, you will always eventually reach the number one.

例如,从数字7开始。它是奇数,所以你给它老3 n + 1治疗,等于22。这是一个偶数,这意味着你必须把它切成一半,这给我们11。这是其他序列的计算:

所以,如果你开始与数字7,Collatz序列是7,22日,11日,34岁,17岁,52岁,26日,13日,40岁,20日,10日,5日,16日,8、4、2、1。如果你再做一次从第一,奇数,你乘以三,添加一个。从那里得到四,迅速降低。这开始循环永不结束。

的另一个名字中生成的数字Collatz猜想是“冰雹序列”。正如你所看到的从上面列出的顺序,数字上升和下降和上下冰雹风暴云,被抛起,收集冰,落入下方云后,再次向上吹。在某种程度上他们下降到地面。有一些数字,一旦你达到他们计算,下降最快,但最终他们都下降。

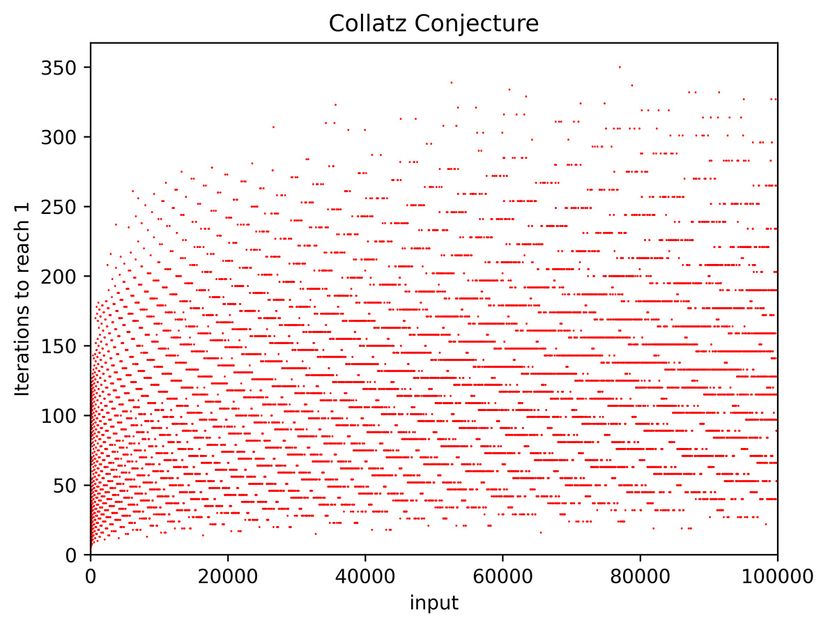
所以Collatz猜想是百万计的数字——任何少于19位数,如果你想尝试你的运气更小,但数学家正在努力解决的问题之一为什么。如果他们知道,他们会说肯定的一种方式,它适用于所有的自然数。

使Collatz猜想如此混淆的一件事是,它涉及一个无限数量的整数。即使是最强大的超级计算机不能检查每一个数字猜想是否适用。没有,至少。

一个数学家近年来取得了一个突破Collatz猜想。特伦斯道最天才的数学家之一,过去的一个世纪,在2019年发表了一篇题为“几乎所有Collatz轨道达到几乎有界值。“道没有无精打采,他21岁的普林斯顿大学获得博士学位,成为历史上最年轻的数学教授在加州大学洛杉矶分校24。他赢得了菲尔兹奖,最高的数学奖的所有土地,31岁。然而他大新闻对他Collatz突破有两个“几乎”。

基本上,道的结果指向一个接近问题的新方法和注意,罕见的是许多偏离Collatz法则。18新利最新登入罕见,但不一定是不存在的。

朋友,是最接近任何人的近年来解决Collatz猜想。记住,如果你要设法解决它自己,从数字开始至少20位数。