几个世纪以前,人类仰望夜空,想象着一个黑色的球体笼罩着地球地球.他们相信星星不过是点状的光。的太阳,月亮其他行星以一种规则而完美的模式围绕地球运行。在他们的思想中,宇宙很小,以地球为中心,被组织成完美的球体。
哥白尼和伽利略等科学家发现了这种哲学的缺陷。在伽利略的发现之后,世界花了一个多世纪的时间才接受地球不是宇宙的中心。随着时间的推移,我们开始对宇宙有了更多的了解。今天,我们通过advanced来研究宇宙望远镜,卫星和调查。
广告
现在我们有图像星系离地球数百万光年远科学家定期研究遥远的恒星。他们甚至发现了行星太阳能系统远远超过我们自己。
但大局如何呢?我们对整个宇宙了解多少?它在膨胀吗?它是无限的吗?如果它不是无限的,那么在空间边界之外的是什么?太空到底是什么样子的?
这些问题属于……的范畴宇宙学研究宇宙的学科。人们尝试了许多不同的方法来研究宇宙。一些人专注于数学。其他人更喜欢使用物理学。相当多的人采取了哲学的方法。
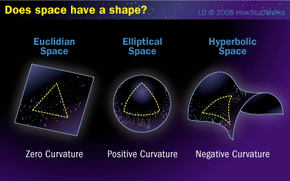
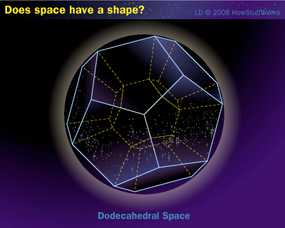
宇宙学家对太空的样子没有共识,但有很多理论。描述空间的挑战之一是很难将其形象化。我们习惯于考虑二维空间中的位置。例如,您可以使用经度和纬度在地图上确定您的位置。但是空间是四维的。你不仅要在长度和宽度的维度上增加深度,你还必须增加时间.事实上,许多宇宙学家把这个维度集合称为时空.
有哪些主要的理论可以帮助我们弄清楚空间的形状?往下读吧。
广告