宇宙中是否存在一个神奇的方程式?也许不是,但有一些我们在自然界中反复发现的非常常见的。以斐波那契数列为例,斐波那契数列是一系列数字和相应的比率,反映了自然界中发现的各种模式,从松果种子的漩涡到鹦鹉螺壳的曲线,再到飓风的扭曲。
人类可能在几千年前就知道这个数字序列了——它可以在古梵文文本中找到——但在现代,我们把它与一个中世纪男人对兔子的痴迷联系在一起。
广告
1202年,意大利数学家莱昂纳多·皮萨诺(又名莱昂纳多·皮萨诺)斐波那契(意为“波纳奇之子”)想知道一组父母能生出多少只兔子。18新利最新登入更具体地说,他提出了一个问题:在最佳条件下,一对兔子在一年内可以繁殖出多少对兔子?18新利最新登入这个思想实验表明,雌性兔子总是生一对,每一对由一只雄性和一只雌性组成[来源:Ghose用]。
想想看:两只刚出生的兔子被放在一个有围栏的院子里,让它们像兔子一样繁殖。兔子至少要到1个月大的时候才能生育后代,所以在第一个月里,只剩下一对。在第二个月的月底,雌性生下一对新的,总共留下两对。当第三个月到来时,原来的一对兔子又生了一对新生儿,而它们早期的后代则长大成人。这样就剩下三对兔子,其中两对将在下个月再生两对,总共是五对兔子。
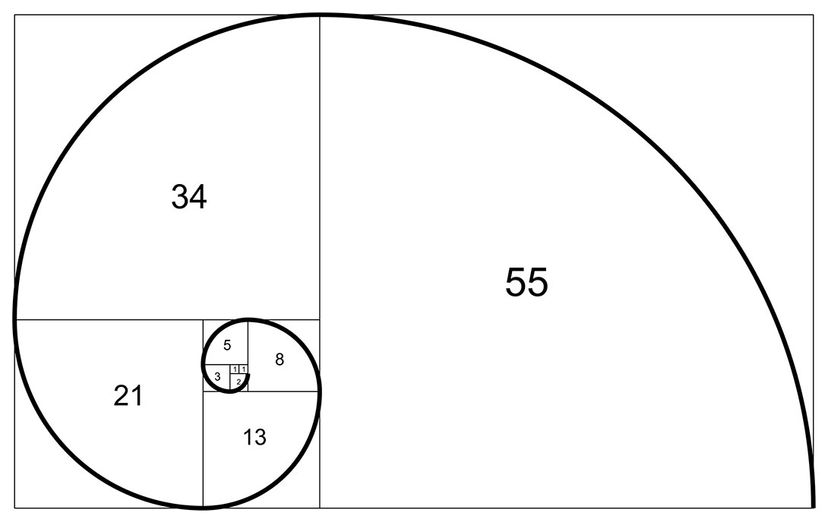
第一个斐波那契数是这样的:0、1、1、2、3、5、8、13、21、34、55、89、144,一直到无穷大。描述它的方程是这样的:Xn+2= Xn+1 + Xn。基本上,每个整数都是前两个数字的和。这个无穷和的集合被称为斐波纳契数列或者是斐波那契序列.斐波那契数列中数字之间的比值(1.6180339887498948482…)通常被称为斐波那契数列黄金比例或金数.连续斐波那契数的比率接近黄金比例,因为数字接近无穷大。
想看看这些迷人的数字在自18新利最新登入然界中是如何表达的吗?不需要去当地的宠物店;你所要做的就是看看你周围。
广告