科学与自然:分形

最著名的分形了曼德尔勃特集合。数学家Benoit Mandelbrot创造了“分形”这个词在1975年命名一个新的类别的数学量化在看似混乱的形状几何不规则和订单。

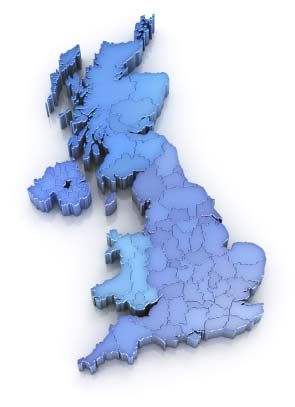
曼德布洛特给了分形几何的名字之前,数学家是应对与分形维数的概念。在研究英国海岸上半年的20世纪,意识到名叫Richardson尺越小,时间越长海岸线测量。作为测量工具减少,它能够捕捉更多的锯齿形状的轮廓的细节。以分形计算,英国海岸线是无限的。

门格尔的海绵是由卡尔·门格尔而探索拓扑维数的量化。艺术的可能低于大多数曼德布洛特和茱莉亚的图像集,但使用海绵门格尔公式拥有先进科学的许多领域。

自然是含有分形形状。这蕨叶展览分形的关键特征之一:自相似性。每个小传单蜷缩成一个模仿大叶的形状。

鹦鹉螺壳是大自然的一个例子展示了她的几何技巧。18新利最新登入每个室是一个较小的迭代它前面的一个;在分形几何公式,这个特点是表示为一个反馈回路,一个迭代的结果为下一次迭代公式变成一个变量。

吃你的几何!Romansco花椰菜生长在这样一个结构化的重复模式,你可能倾向于认为这样做的工程被邪恶科学家倾向于蔬菜统治。不!负责所有的数学性质。

密切关注雪花,你会发现每个分支的特点它的形状看起来一样的薄片作为一个整体(至少直到融化)。发现并量化这些有序结构在最初出现随机是分形几何的主要目标之一。

这不是一个放大的雪花;这是一个分形方程可视化表示。自然产生的分形的相似性和创建数学说明密切相关的两个分支的几何学。

而自然提供了无数的分形可爱的例子,一旦分形公式表达视觉策划他们的价值观在复数平面上,一个新的艺术流派诞生了。

数学家加斯顿是茱莉亚创生的反馈回路的概念用于分形几何。他的工作在1900年代早期被缺乏计算机执行有限的计算公式,茱莉亚集。今天,数码艺术家使用茱莉亚组的变化创造的艺术作品。想象一下茱莉亚与21世纪的计算能力会做!

通过改变分形方程中的变量,您可以创建无限变化的主题。如果你仔细看看这张图片,你会看到越来越小了曼德尔勃特集合的迭代。

你看的视觉表征分形方程,你开始看到自然的“混乱”。18新利最新登入这个分形的蓝色渲染很容易看到它的相似之处一个崎岖的海岸线。

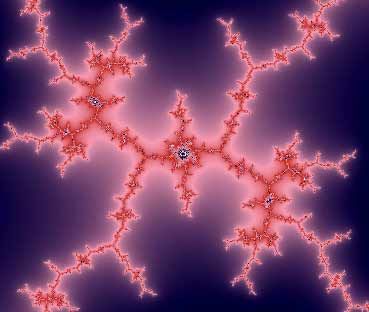
画Mendelbrot集的变化往往段闪光像卷须,这是巧合——闪电是一种自然产生的分形。

如果你要放大的小手臂呈现的茱莉亚,你会看到,他们看起来完全像更大的图像。这种自相似性无限在计算机生成的分形模型,而分形通常发生在自然运行通过有限数量的迭代。

还记得那些隐藏的图像中的话,在1990年代这么受欢迎?如果你盯着看似忙碌,重复模式,最终3 - d图像应该成为可见。这些艺术作品的创作者使用分形作为他们的背景的基础。这张照片好像可以立体,但事实上它只是一个正常的分形。

最后,分形几何的一个例子可以既美观实用。18新利最新登入这户外展示了使用分形来创建一个散热遮阳伞在东京。使用分形角度由四面体驱散热量比平顶阴影更有效。了解更多关于18新利最新登入分形是如何工作的。